Accelerating QP optimization with RLQP
In order to automatically select \(\rho\), RLQP learns a policy to automatically adapt a single scalar \(\bar{\rho}\) value to be used for all constraints. Integrating this policy into solvers is straightforward as the current heuristic in OSQP already generates a single scalar adaptation. This policy also can simply check that the proposed change to \(\bar\rho\) is sufficiently small and avoid a costly matrix factorization.
In both handcrafted and RL cases, the policy is a function \(\pi : S_{\bar\rho} \rightarrow A_{\bar\rho}\), where \(S_{\bar\rho} \in \mathbb{R}^2\) are the primal and dual residuals stacked into a vector, \(A_{\bar\rho} \in \mathbb{R}\) is the value to set to \(\bar\rho\). The observation space and action space closely reflect what the current heuristic considers in QP solvers.
This simple scalar policy outperforms the handwritten heuristic in OSQP. However, this simple policy does not consider variations in how \(\rho\) should be adapted across constraints. However, it is not clear how to craft a policy for a simple vectorized environment while supporting problems with a variable number of constraints. Ideally, a policy will consider an observation space of all residuals with an action space to predict all \(\rho\) values at once. However, this policy would need to be trained for a particular number of constraints and would not adapt to arbitrary problems. The
Instead, we consider a reformulation of the vectorized environment as a multi-agent partially-observed MDP. Given a QP with \(m\) constraints, we factorize the global policy into \(m\) indepentent policies that consider observations for a single constraint and predict a single \(\rho_i\) value. Therefore, the observation spaces and action spaces for these policies are fully indepentent from each other. We then share parameters for the policy across all constraints. Remarkably, we find the vector policy generalizes to problems with more constraints than seen during training.
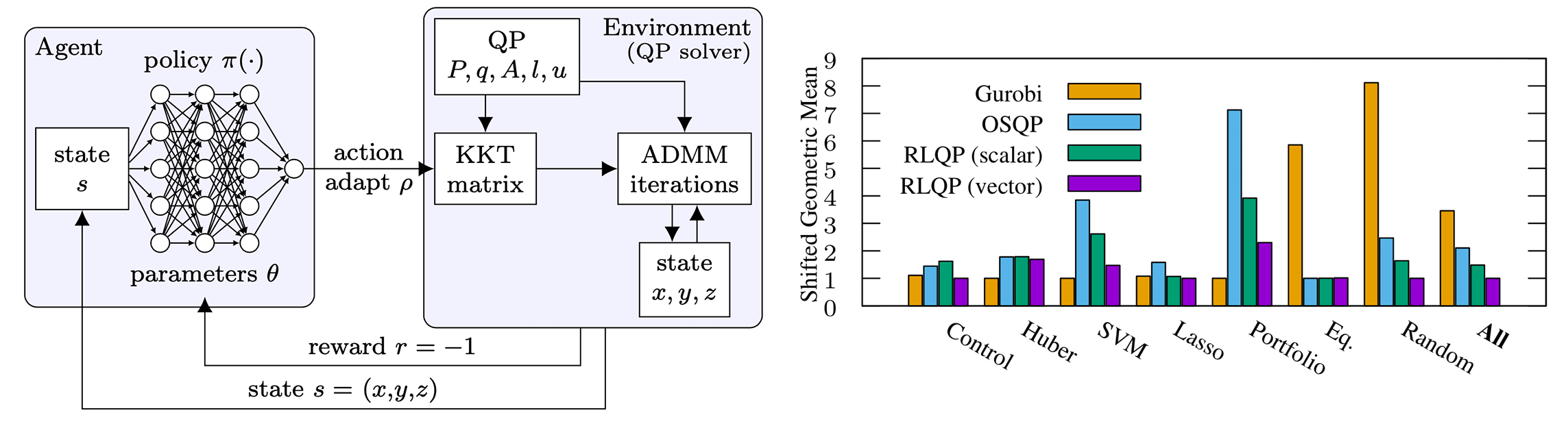 We demonstrate reinforcement learning can significantly accelerate first-order optimization, outperforming state-of-the-art solvers by up to 3x. RLQP avoids suboptimal heuristics within solvers by tuning the internal parameters of the ADMM algorithm. By decomposing the policy as a multi-agent partially observed problem, RLQP adapts to unseen problem classes and to larger problems than seen during training.
We demonstrate reinforcement learning can significantly accelerate first-order optimization, outperforming state-of-the-art solvers by up to 3x. RLQP avoids suboptimal heuristics within solvers by tuning the internal parameters of the ADMM algorithm. By decomposing the policy as a multi-agent partially observed problem, RLQP adapts to unseen problem classes and to larger problems than seen during training.